数组相关

二分法（折半查找）

二分查找从入门到入睡 - 力扣（LeetCode）

循环不变量原则，返回 r 还是 l 的逻辑是：

  • 你知道while结束后 l 或 r的左侧元素或右侧元素分别满足什么「循环关系」。
  • 你知道l与r的位置关系。（只有两种情况，模版一就是 r = l - 1，模版二就是 l = r）
  • 你知道题目要求你返回什么。

这三点你都知道了，你就知道该返回什么了。

  • 建议大家在书写二分查找代码时保持同一种风格和习惯（先更新 \(l\) 再更新 \(r\) 的形式)，这样能够减少思考负担。

二分查找算法中的四要素为：初始值、循环条件、\(c\) 的计算方式、左右界更新语句。此四要素的有机结合，构成了具体的二分模版形式。

四要素的 约束 。

对于二分查找的任意模版:

  • \(while\) 中的不等号和 \(l, r\) 的更新语句决定了二分搜索循环终止时 \(l\) 与 \(r\) 的位置关系（相错 / 相等 / 相邻）。

  • \(l, r\) 的初始值和 \(c\) 的计算方式要使得中间下标 \(c\) 覆盖且仅覆盖「搜索空间」中所有可能的下标。

模版初始值
\(n : nums.length\)		循环条件中间值下标 \(c\)左右界
模版一
相错终止		\(l = 0, r = n - 1\)
\([l, r]\) 左闭右闭		\(while(l <= r)\)\(c = l + (r - l) / 2\)
下取整		\(l = c + 1\)
\(r = c - 1\)
模版二
相等终止		\(l = 0, r = n\)
\([l, r)\) 左闭右开		\(while(l < r)\)\(c = l + (r - l) / 2\)
下取整		\(l = c + 1\)
\(r = c\)
模版二
相等终止		\(l =-1, r = n - 1\)
\((l, r]\) 左开右闭		\(while(l < r)\)\(c = l + (r - l+1) / 2\)
上取整		\(l = c\)
\(r = c - 1\)
模版三
相邻终止		\(l = -1, r = n\)
\((l, r)\) 左开右开		\(while(l+1 < r)\)\(c = l + (r - l) / 2\)
下取整		\(l = c\)
\(r = c\)


四种情况均可转化为 大于等于≥ 的情况

  • 大于等于≥x
  • 大于 ＞x ==> ≥x+1
  • 小于＜x ==> ≥x-1
  • 小于等于≤x ==> ＞x+1

模板一：左闭右闭，相错终止

情形1 (大于等于)

1
2
3
4
5
6
7
8
9
10
11
12
13
// 模版一「一般」情形1: 大于等于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while(l <= r){
            int c = l + (r - l) / 2;
            if(nums[c] < target) l = c + 1; // #1 更新后l左侧元素「必」小于target
            else r = c - 1; // #2 更新后r右侧「必」大于等于target
        }
        // return (l == nums.length || nums[l] != target) ? -1 : l; // 704题的返回，处理:相等/不等
        return l == nums.length ? -1 : l; // 处理: 相等/刚好大于/不存在
    }
}
  1. 对于 #1 行，若进入该分支，则 \(l\) 下标更新后其左侧元素「必」 小于  \(target\) 。
  2. 对于 #2 行，若进入该分支，则 \(r\) 下标更新后其右侧元素「必」 大于等于  \(target\) 。
  • 返回值：一个判断即可对应三种情况 (后两种都返回 \(l\) )。另外，因为 \(r+1 = l\)，用 \(l\) 或 \(r+1\) 来返回都是可以的。

情形2 (大于)

「情形2」考虑 \(target\) 的三种情况：

  • \(nums\) 中所有元素都小于 \(target\) 时，\(r\) 不更新，最终 \(l = nums.length\)，因此当这个关系成立时，返回 -1。
  • \(nums\) 中存在元素大于 \(target\) 时，由两条「循环不变」关系可知应返回 \(l\) ( \(r\) 的右侧)。
  • \(nums\) 中所有元素都大于 \(target\) 时，\(l\) 不更新，\(l = 0\) ，此时应当返回下标0，因此返回 \(l\) 。

「情形2」与「情形1」只有一个 '=' 字符的差别。事实上这些代码都十分相似，但差之毫厘谬以千里，需要谨慎对待。

1
2
3
4
5
6
7
8
9
10
11
12
// 模版一「一般」情形2: 大于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while(l <= r){
            int c = l + (r - l) / 2;
            if(nums[c] <= target) l = c + 1; // #1 更新后l左侧元素「必」小于等于target
            else r = c - 1; // #2 更新后r右侧「必」大于target
        }
        return l == nums.length ? -1 : l; // 处理: 刚好大于/不存在
    }
}

情形3 (小于等于)

「情形3」考虑 \(target\) 的三种情况：

  • \(nums\) 中所有元素都小于 \(target\) 时，应当返回最大下标 \(nums.length - 1\)，\(r\) 未更新，仍有 \(r = nums.length - 1\)，因此返回 \(r\)。
  • \(nums\) 中存在元素小于等于 \(target\) 时，由两条「循环不变」关系可知应返回 \(r\) ( \(l\) 的左侧)。
  • \(nums\) 中所有元素都大于 \(target\) 时，\(l\) 不更新，\(l = 0\) ，此时应当返回 -1，而此时刚好有 \(r = -1\) ，因此返回 \(r\)。

三种情况都返回 \(r\)。但若用此情形处理704题，则需调整，请参考注释行。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 模版一「一般」情形3: 小于等于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while(l <= r){
            int c = l + (r - l) / 2;
            if(nums[c] <= target) l = c + 1; // #1 更新后l左侧「必」小于等于target
            else r = c - 1; // #2 更新后r右侧「必」大于target
        }
        // return (r == -1 || nums[r] != target) ? -1 : r; // 704题的返回，处理:相等/不等
        return r; // 处理: 相等/刚好小于/不存在
    }
}

情形4 (小于)

「情形4」考虑 \(target\) 的三种情况：

  • \(nums\) 中所有元素都小于 \(target\) 时，应当返回最大下标 \(nums.length - 1\)，\(r\) 未更新，仍有 \(r = nums.length - 1\)，因此返回 \(r\)。
  • \(nums\) 中存在元素小于 \(target\) 时，由两条「循环不变」关系可知应返回 \(r\) ( \(l\) 的左侧)。
  • \(nums\) 中所有元素都大于等于 \(target\) 时，\(l\) 不更新，\(l = 0\)，此时应当返回 -1，而刚好有 \(r = -1\)，因此返回 \(r\)。

三种情况都返回 \(r\)，「情形4」与「情形3」只有一个 '=' 字符的差别。

1
2
3
4
5
6
7
8
9
10
11
12
// 模版一「一般」情形4: 小于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while(l <= r){
            int c = l + (r - l) / 2;
            if(nums[c] < target) l = c + 1; // #1 更新后l左侧元素「必」小于target
            else r = c - 1; // #2 更新后r右侧「必」大于等于target
        }
        return r; // 处理: 相等/刚好小于/不存在
    }
}

模版一总结

  • 核心在于 「相错终止」 ，即循环终止时有 \(r = l - 1\)。「模版一」的标志是 \(while\) 中的 \(l <= r\) 以及 \(l\) 与 \(r\) 更新时的 \(l = c + 1, r = c - 1\)，二者相辅相成，共同作用实现了「相错终止」。另外 \(l\) 与 \(r\) 的初始取值的 「左闭右闭」 特点也是「模版一」的一个特点。
  • 通过 \(l\) 左侧和 \(r\) 右侧的「循环不变」关系，确定 \(while\) 终止后的目标下标。在「一般」情形中，要考虑 不更新导致的越界 及其对应的返回前判断。
  • 相等或不等的情形都可以用「一般」版本，但相等情形应当用「相等返回」版本，能够在找到相等元素时立即返回结果，一般版本则一定会穷尽二分过程。
  • 通过对「模版一」的分析，得到「四要素」相互配合的「重要结论」，此「重要结论」是 二分查找算法的核心所在 。

模版二：左闭右开，相等终止

情形1 (大于等于)

「情形1」考虑 \(target\) 的三种情况：

  • \(nums\) 中所有元素都小于 \(target\) 时，\(r\) 不更新，最终 \(r = nums.length\)，因此当这个关系成立时，返回 -1。
  • \(nums\) 中存在元素大于等于 \(target\) 时，由两条「循环不变」关系可知应返回 \(r\)。
  • \(nums\) 中所有元素都大于 \(target\) 时，\(l\) 不更新，最终 \(l = r = 0\)，我们需要返回下标 0，而此时 \(r\) 正好等于 0。

一条判断对应三种情况(两个分支)。若用于处理 704 题，返回时的判断需做调整，见注释行。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 模版二「一般」情形1: 大于等于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length;
        while(l < r){
            int c = l + (r - l) / 2;
            if(nums[c] < target) l = c + 1; // #1 更新后l左侧元素「必」小于target 
            else r = c; // #2 更新后r及r右侧「必」大于等于target
        }
        // return (r != nums.length && nums[r] == target) ? r : -1; // 704题的返回，处理:相等/不等
        return r != nums.length ? r : -1; // 处理:等于/刚好大于/不存在
    }
}

情形2 (大于)

「情形2」考虑 \(target\) 的三种情况：

  • \(nums\) 中所有元素都小于等于 \(target\) 时，\(r\) 不更新，最终 \(r = nums.length\)，因此当这个关系成立时，返回 -1。
  • \(nums\) 中存在元素大于 \(target\) 时，由两条「循环不变」关系可知应返回 \(r\)。
  • \(nums\) 中所有元素都大于 \(target\) 时，\(l\) 不更新，最终 \(l = r = 0\)，我们需要返回下标0，而此时 \(r\) 正好等于0。
1
2
3
4
5
6
7
8
9
10
11
12
// 模版二「一般」情形2: 大于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length;
        while(l < r){
            int c = l + (r - l) / 2;
            if(nums[c] <= target) l = c + 1; // #1 更新后l左侧「必」小于等于target 
            else r = c; // #2 更新后r及其右侧「必」大于target
        }
        return r == nums.length ? -1 : r; // 处理:刚好大于/不存在
    }
}

情形3 (小于等于)

1
2
3
4
5
6
7
8
9
10
11
12
13
// 模版二「一般」写法之情形3（正确版1）
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length;
        while(l < r){
            int c = l + (r - l) / 2;
            if(nums[c] < target) l = c + 1; // #1 更新后l左侧元素「必」小于target 
            else r = c; // #2 更新后r及其右侧「必」大于等于target
        }
        // return (r != nums.length && nums[r] == target) ? r : -1; // 704题的返回，处理:相等/不等
        return (r == nums.length || nums[r] != target) ? r - 1 : r; // 处理:相等/刚好小于/不存在
    }
}

这时候我们会发现，不是又变回情形一了吗？没错，直到 \(while\) 结束前的语句，与情形一是完全一致的（因此终止情形也只有 \(l = r\) 一种）。当 \(while\) 结束后，\(l\) 左侧元素必小于 \(target\) ，\(r\) 及其右侧元素必大于等于 \(target\) 。我们只需在返回前调整一下判断，就能返回正确结果了。判断语句经由如下思考后写就。

  • \(nums\) 中所有元素都小于 \(target\) 时，\(r\) 不更新，最终 \(r = nums.length\) ，因此当这个关系成立时，返回 \(r - 1\)。
  • \(nums\) 中存在元素小于等于 \(target\) 时，由两条「循环不变」关系可知，如果 \(nums[r]\)** 等于 \(target\) ，需要返回 \(r\)，否则返回 \(r - 1\)。 **
  • \(nums\) 中所有元素都大于 \(target\) 时，\(l\) 不更新，最终 \(l = r = 0\)，我们需要返回 -1，而此时 \(r - 1\)正好等于 -1。

情形4 (小于)

「情形4」考虑 \(target\) 的三种情况：

  • \(nums\) 中所有元素都小于 \(target\) 时，\(r\) 不更新，最终 \(r = nums.length\)，因此当这个关系成立时，返回 \(r - 1\)。
  • \(nums\) 中存在元素小于 \(target\) 时，由两条「循环不变」关系可知应返回 \(r - 1\) 。
  • \(nums\) 中所有元素都大于等于 \(target\) 时，\(l\) 不更新，最终 \(l = r = 0\) ，我们需要返回 -1，而此时 \(r - 1\) 正好等于 -1。
1
2
3
4
5
6
7
8
9
10
11
12
// 模版二「一般」情形4: 小于
class Solution {
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length;
        while(l < r){
            int c = l + (r - l) / 2;
            if(nums[c] < target) l = c + 1; // #1 更新后l左侧元素「必」小于target 
            else r = c; // #2 更新后r及其右侧「必」大于等于target
        }
        return r - 1; // 处理:刚好小于/不存在
    }
}

二分题单

转载：https://github.com/SharingSource/LogicStack-LeetCode/wiki/%E4%BA%8C%E5%88%86

题目题解难度推荐指数
4. 寻找两个正序数组的中位数LeetCode 题解链接困难🤩🤩🤩🤩
29. 两数相除LeetCode 题解链接中等🤩🤩🤩
33. 搜索旋转排序数组LeetCode 题解链接中等🤩🤩🤩🤩🤩
34. 在排序数组中查找元素的第一个和最后一个位置LeetCode 题解链接中等🤩🤩🤩🤩🤩
35. 搜索插入位置LeetCode 题解链接简单🤩🤩🤩🤩🤩
74. 搜索二维矩阵LeetCode 题解链接中等🤩🤩🤩🤩
81. 搜索旋转排序数组 IILeetCode 题解链接中等🤩🤩🤩🤩
153. 寻找旋转排序数组中的最小值LeetCode 题解链接中等🤩🤩🤩
154. 寻找旋转排序数组中的最小值 IILeetCode 题解链接困难🤩🤩🤩
162. 寻找峰值LeetCode 题解链接中等🤩🤩🤩🤩🤩
209. 长度最小的子数组LeetCode 题解链接中等🤩🤩🤩🤩🤩
215. 数组中的第K个最大元素LeetCode 题解链接中等🤩🤩🤩
220. 存在重复元素 IIILeetCode 题解链接中等🤩🤩🤩
240. 搜索二维矩阵 IILeetCode 题解链接中等🤩🤩🤩🤩🤩
274. H 指数LeetCode 题解链接中等🤩🤩🤩
275. H 指数 IILeetCode 题解链接中等🤩🤩🤩
278. 第一个错误的版本LeetCode 题解链接简单🤩🤩🤩🤩
334. 递增的三元子序列LeetCode 题解链接中等🤩🤩🤩🤩
352. 将数据流变为多个不相交区间LeetCode 题解链接困难🤩🤩🤩🤩
354. 俄罗斯套娃信封问题LeetCode 题解链接困难🤩🤩🤩
363. 矩形区域不超过 K 的最大数值和LeetCode 题解链接困难🤩🤩🤩
367. 有效的完全平方数LeetCode 题解链接简单🤩🤩🤩🤩🤩
373. 查找和最小的K对数字LeetCode 题解链接中等🤩🤩🤩🤩🤩
374. 猜数字大小LeetCode 题解链接简单🤩🤩🤩
436. 寻找右区间LeetCode 题解链接中等🤩🤩🤩🤩
441. 排列硬币LeetCode 题解链接简单🤩🤩🤩
449. 序列化和反序列化二叉搜索树LeetCode 题解链接中等🤩🤩🤩🤩
475. 供暖器LeetCode 题解链接中等🤩🤩🤩🤩
497. 非重叠矩形中的随机点LeetCode 题解链接中等🤩🤩🤩🤩🤩
528. 按权重随机选择LeetCode 题解链接中等🤩🤩🤩🤩
532. 数组中的 k-diff 数对LeetCode 题解链接中等🤩🤩🤩🤩
540. 有序数组中的单一元素LeetCode 题解链接中等🤩🤩🤩🤩
611. 有效三角形的个数LeetCode 题解链接中等🤩🤩🤩🤩
646. 最长数对链LeetCode 题解链接中等🤩🤩🤩🤩🤩
658. 找到 K 个最接近的元素LeetCode 题解链接中等🤩🤩🤩🤩
668. 乘法表中第k小的数LeetCode 题解链接困难🤩🤩🤩🤩🤩
704. 二分查找LeetCode 题解链接简单🤩🤩🤩🤩🤩
710. 黑名单中的随机数LeetCode 题解链接困难🤩🤩🤩🤩
719. 找出第 K 小的数对距离LeetCode 题解链接困难🤩🤩🤩🤩
728. 自除数LeetCode 题解链接简单🤩🤩🤩
744. 寻找比目标字母大的最小字母LeetCode 题解链接简单🤩🤩🤩🤩🤩
778. 水位上升的泳池中游泳LeetCode 题解链接困难🤩🤩🤩
786. 第 K 个最小的素数分数LeetCode 题解链接中等🤩🤩🤩
793. 阶乘函数后 K 个零LeetCode 题解链接困难🤩🤩🤩🤩
852. 山脉数组的峰顶索引LeetCode 题解链接简单🤩🤩🤩🤩🤩
875. 爱吃香蕉的珂珂LeetCode 题解链接中等🤩🤩🤩🤩
911. 在线选举LeetCode 题解链接中等🤩🤩🤩🤩🤩
926. 将字符串翻转到单调递增LeetCode 题解链接中等🤩🤩🤩
981. 基于时间的键值存储LeetCode 题解链接中等🤩🤩🤩🤩
1004. 最大连续1的个数 IIILeetCode 题解链接中等🤩🤩🤩
1011. 在 D 天内送达包裹的能力LeetCode 题解链接中等🤩🤩🤩🤩
1044. 最长重复子串LeetCode 题解链接困难🤩🤩🤩🤩
1175. 质数排列LeetCode 题解链接简单🤩🤩🤩🤩
1208. 尽可能使字符串相等LeetCode 题解链接中等🤩🤩🤩
1235. 规划兼职工作LeetCode 题解链接困难🤩🤩🤩🤩
1337. 矩阵中战斗力最弱的 K 行LeetCode 题解链接简单🤩🤩🤩
1414. 和为 K 的最少斐波那契数字数目LeetCode 题解链接中等🤩🤩🤩🤩
1438. 绝对差不超过限制的最长连续子数组LeetCode 题解链接中等🤩🤩🤩
1482. 制作 m 束花所需的最少天数LeetCode 题解链接中等🤩🤩🤩
1608. 特殊数组的特征值LeetCode 题解链接简单🤩🤩🤩🤩🤩
1640. 能否连接形成数组LeetCode 题解链接简单🤩🤩🤩
1707. 与数组中元素的最大异或值LeetCode 题解链接困难🤩🤩🤩
1713. 得到子序列的最少操作次数LeetCode 题解链接困难🤩🤩🤩
1751. 最多可以参加的会议数目 IILeetCode 题解链接困难🤩🤩🤩
1818. 绝对差值和LeetCode 题解链接中等🤩🤩🤩🤩🤩
1838. 最高频元素的频数LeetCode 题解链接中等🤩🤩🤩
1894. 找到需要补充粉笔的学生编号LeetCode 题解链接中等🤩🤩🤩🤩
1984. 学生分数的最小差值LeetCode 题解链接简单🤩🤩🤩🤩🤩
2055. 蜡烛之间的盘子LeetCode 题解链接中等🤩🤩🤩🤩
剑指 Offer 04. 二维数组中的查找LeetCode 题解链接中等🤩🤩🤩🤩🤩
剑指 Offer 11. 旋转数组的最小数字LeetCode 题解链接简单🤩🤩🤩🤩
剑指 Offer 53 - I. 在排序数组中查找数字 ILeetCode 题解链接简单🤩🤩🤩🤩🤩
剑指 Offer 53 - II. 0～n-1中缺失的数字LeetCode 题解链接简单🤩🤩🤩🤩🤩
剑指 Offer II 008. 和大于等于 target 的最短子数组LeetCode 题解链接中等🤩🤩🤩🤩
剑指 Offer II 069. 山峰数组的顶部LeetCode 题解链接简单🤩🤩🤩🤩🤩

排序相关

归并排序

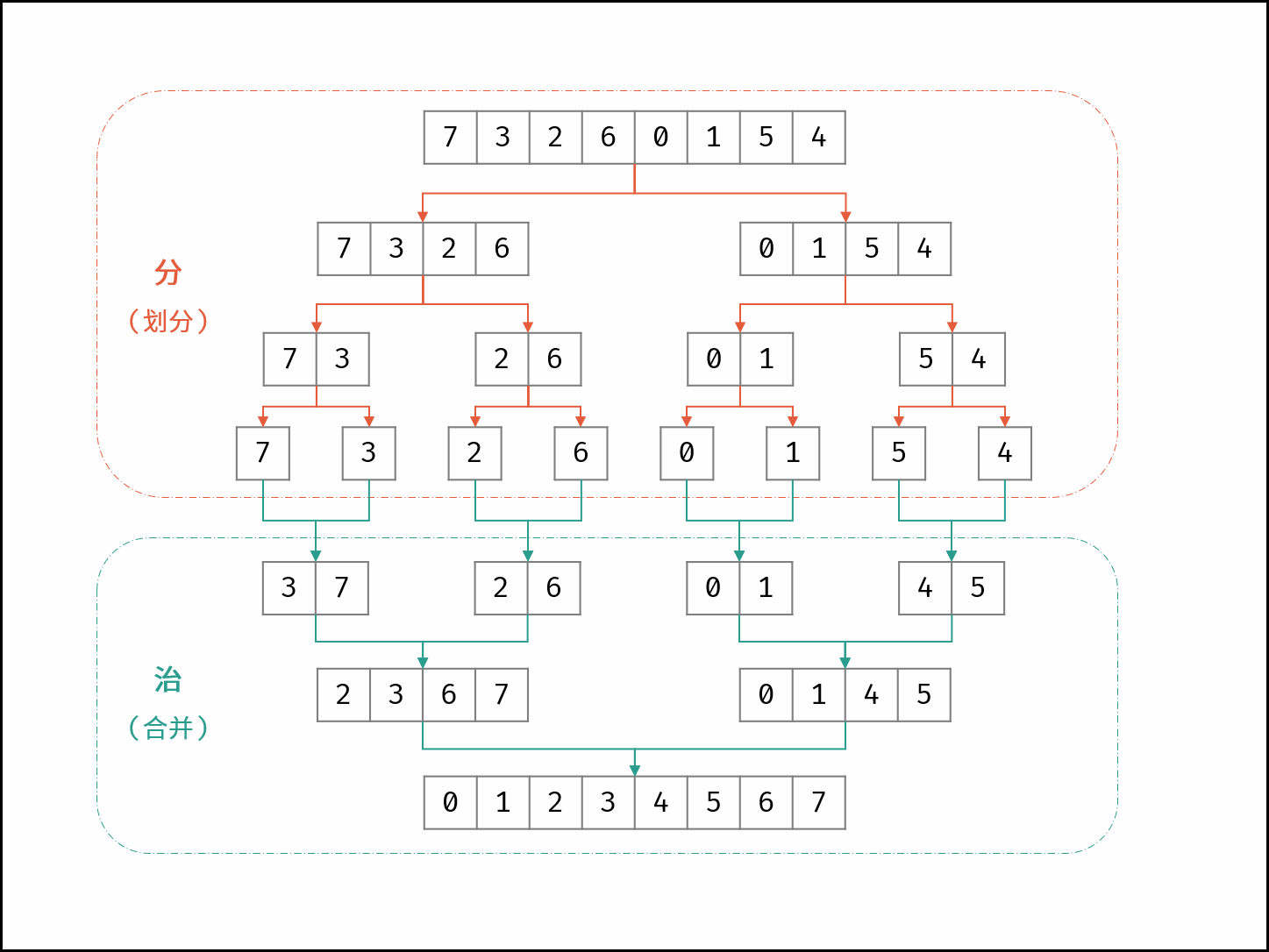
归并排序体现了 “分而治之” 的算法思想，合并阶段 本质上是 合并两个排序数组 的过程，具体为：

  • 分： 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
  • 治： 划分到子数组长度为 1 时，开始向上合并，不断将 较短排序数组 合并为 较长排序数组，直至合并至原数组时完成排序；

如下图所示，为数组 [7, 3, 2, 6, 0, 1, 5, 4] 的归并排序过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public class Solution {
    public static void main(String[] args) {
        int[] nums = {7, 3, 2, 6, 0, 1, 5, 4};
        mergeSort(nums, 0, nums.length-1);
        for(int i : nums) System.out.println(i);
    }
    public static void mergeSort(int[] nums,int left,int right){
        //当只有一个节点的时候，直接返回，退出递归
        if(left >= right){
            return;
        }
        int mid = (left+right)/2;
        //左拆分
        mergeSort(nums,left,mid);
        //右拆分
        mergeSort(nums,mid+1,right);
        //合并
        merge(nums,left,mid,right);
    }
    public static void merge(int[] nums,int left,int mid,int right){
        //定义一个临时数组
        int[] temp = new int[right-left+1];
        //定义一个指针，指向第一个数组的第一个元素
        int i = left;
        //定义一个指针，指向第二个数组的第一个元素
        int j = mid+1;
        //定义一个指针，指向临时数组的第一个元素
        int t = 0;
        //当两个数组都有元素的时候，遍历比较每个元素大小
        while(i <= mid && j <= right){
            //比较两个数组的元素，取较小的元素加入到，临时数组中
            //并将两个指针指向下一个元素
            if(nums[i] <= nums[j]){
                temp[t++] = nums[i++];
            }else{
                temp[t++] = nums[j++];
            }
        }
        //当左边的数组没有遍历完成后，直接将剩余元素加入到临时数组中
        while(i <= mid){
            temp[t++] = nums[i++];
        }
        //当右边的数组没有遍历完成后，直接将剩余元素加入到临时数组中
        while(j <= right){
            temp[t++] =nums[j++];
        }
        //将新数组中的元素，覆盖nums旧数组中的元素。
        //此时数组的元素已经是有序的
        for(int k =0; k< temp.length;k++){
            nums[left+k] = temp[k];
        }
    }
}

例题：剑指 Offer 51. 数组中的逆序对

树形结构相关

树状数组（二叉索引树）

IndexTree适用范围：

求区间和或区间极值（最大最小值）；

解决LIS问题。

涉及到动态排序时，可能适用；（也可以考虑使用PQ）

涉及到双指针（区间问题）时，可能适用；

涉及到散列化时，可能适用；

涉及到需要捆绑下标排序的相关问题时，可能适用。

BIT可以解决的问题，Index Tree都可以解决；Index Tree可以解决的问题，线段树都可以解决。

参考：IndexTree及AC自动机

​ 树状数组是一种实现了高效查询「前缀和」与「单点更新」操作的数据结构，IndexTree所能解决的典型问题就是存在一个长度为n的数组【如何高效的求某一个范围内的前缀和】,智能的解决单点更新完怎么维护一个结构快速查询的一个累加和的问题，其基本操作主要有：

  1. int sum(int index)求1到index位置都累加和
  2. void add(int index, int d) 将index位置的数加一个d
  3. int RangeSum(int index1, int index2) 求index1到index2上面的累加和

树状数组或二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树。其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和。它可以以O(logn)的时间得到任意前缀和，并同时支持在O(logn)时间内支持动态单点值的修改。空间复杂度O(n)

问题1：如何获取一个二进制序列中最右侧的1？

公式：n&(~n+1) == n&(-n)

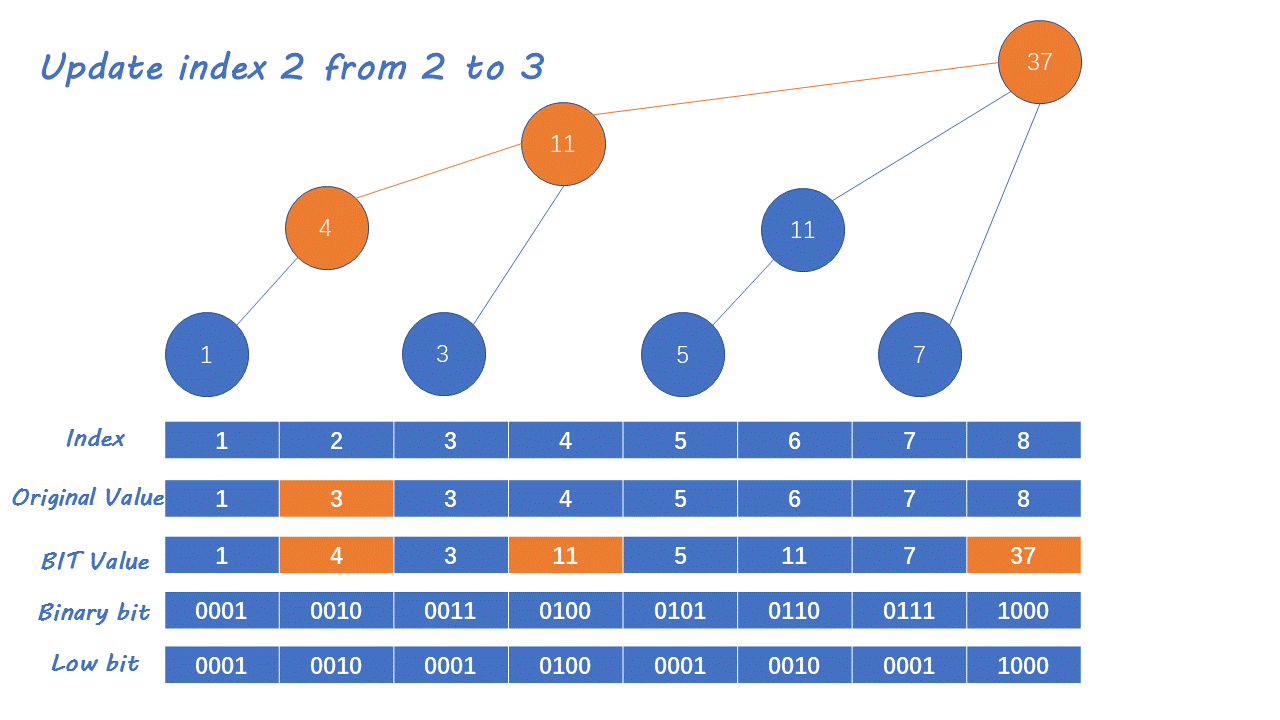
在IndexTree中一般有一个helper数组对应i为位置管理了一段区间的累加和：举个例子

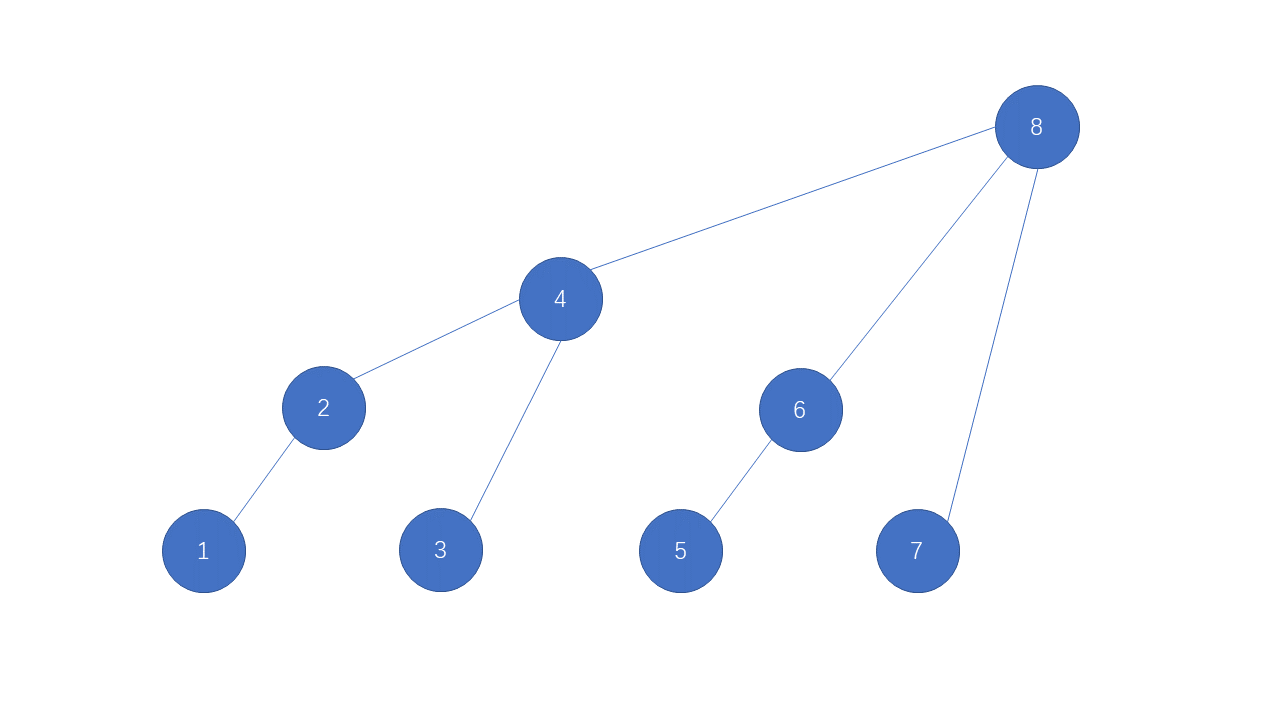
那么，假设有序列A = {1, 2, 3, 4, 5, 6, 7, 8}，注意在help数组中0位置不用，从1位置开始。1位置管理1位置的元素，2位置往前一看1位置有一个和我长度一模一样的累加和于是2位置就管理1-2位置的累加和。3位置一看前面只有没有和他一样长度的累加和，所以3就只能管理3位置的数字了，4位置一看前面有一个3是和我长度一样的，于是他们两就结成伴了长度就变成2了往前一看还有一个长度为1-2的，于是他们两就结合在一起了，所以4位置管理的是1~8位置的累加和，同理5 6 7 8 位置也可以按照相同的方法求出，这样我们就得到了help数组

对应树形结构：

​ sum(int index)：假设我们想知道help数组中8位置对应位置管理的是哪个范围的累加和：首先我们只需要将8的二进制序列写出来 1000，我们将它最右边的1消掉在将这个数加1：也就是0000+1=0001他管理的范围就是消去最右边1的数+1到他本身也就是1~8.不信我们在尝试一个6：它对应的二进制序列为110，将其最右侧的1消去在加1得到101也就是5到6.

​ add(int index, int d)：如果某一位置的值加上了某个数，必然会引起其他位置的值发生变化那么那些位置的值会发生变化呢？首先自己这个位置肯定会发生变化，其他位置通过计算得到，同样的先把其二进制序列写出来，将最右侧的1去出来和原来的数相加得到数就是会发生变化的位置，再重复上面这个过程，直到它大于n就结束。将对应位置的值加上这个数即可这样我们就更新完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 下标从1开始！
public static class IndexTree {

    private int[] tree;
    private int N;

    // 0位置弃而不用！
    public IndexTree(int size) {
        N = size;
        tree = new int[N + 1];
    }

    // 1~index 累加和是多少？
    public int sum(int index) {
        int ret = 0;
        while (index > 0) {
            ret += tree[index];
            index -= index & -index;
        }
        return ret;
    }

    // index & -index : 提取出index最右侧的1出来
    // index :           0011001000
    // index & -index :  0000001000
    public void add(int index, int d) {
        while (index <= N) {
            tree[index] += d;
            index += index & -index;
        }
    }
    
    public int RangeSum(int index1, int index2) {//求范围和
		return sum(index2) - sum(index1);
	}
}

例题：剑指 Offer 51. 数组中的逆序对

线段树

字典树Trie

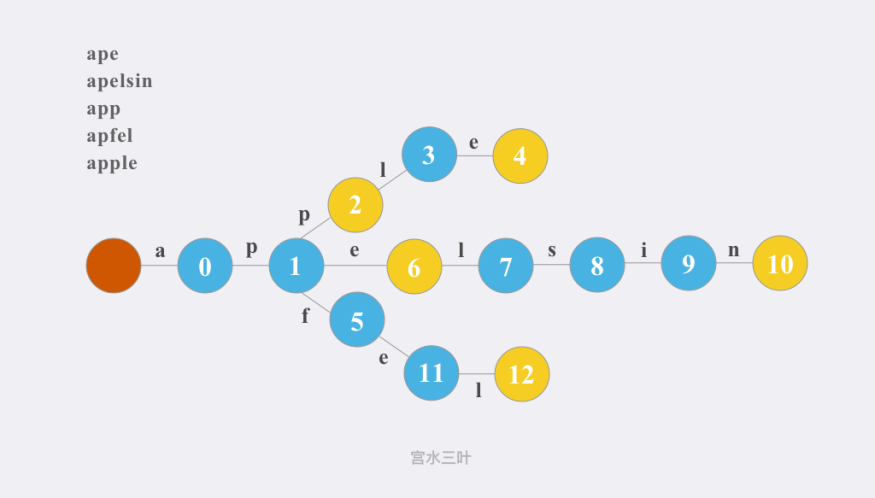
Trie树（又叫「前缀树」或「字典树」）是一种用于快速查询「某个字符串/字符前缀」是否存在的数据结构。

其核心是使用「边」来代表有无字符，使用「点」来记录是否为「单词结尾」以及「其后续字符串的字符是什么」。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Trie {
    class TrieNode{//字典树的结点数据结构
		boolean end;//是否是单词末尾的标识
		TrieNode[] child; //26个小写字母的拖尾
		public TrieNode(){
			end = false;
			child = new TrieNode[26];
		}
	}

	TrieNode root;//字典树的根节点。
	
    public Trie() {
        root = new TrieNode();
    }

    public void insert(String s) {
        TrieNode p = root;
        for(int i = 0; i < s.length(); i++) {
            int u = s.charAt(i) - 'a';
			//若当前结点下没有找到要的字母，则新开结点继续插入
            if (p.child[u] == null) p.child[u] = new TrieNode();
            p = p.child[u]; 
        }
        p.end = true;
    }

    public boolean search(String s) {
        TrieNode p = root;
        for(int i = 0; i < s.length(); i++) {
            int u = s.charAt(i) - 'a';
            if (p.child[u] == null) return false;//变化点（根据题意）
            p = p.child[u]; 
        }
        return p.end;
    }

    public boolean startsWith(String s) {
        TrieNode p = root;
        for(int i = 0; i < s.length(); i++) {
            int u = s.charAt(i) - 'a';
            if (p.child[u] == null) return false;
            p = p.child[u]; 
        }
        return true;
    }
}

例题：792. 匹配子序列的单词数

其他小技巧

最小公倍数和最大公因数

1
2
3
4
5
6
7
8
9
// 求最小公倍数
private long lcm(long a, long b) {
    return a * 1L * (b / gcd(a, b));
}

// 求最大公约数
private long gcd(long a, long b) {
    return b == 0 ? a : gcd(b, a % b);
}

GCD定理：两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。最大公约数（Greatest Common Divisor）缩写为GCD。gcd(a,b) = gcd(b,a mod b) (不妨设a>b 且r=a mod b ,r不为0)

文字不好理解，举个实例： 134 / 18 = 7 … 8 18 / 8 = 2 … 2 8 / 2 = 4 … 0

我们要找最大公约数，而134/18 的和 8/2 的最大公约数相等，所以我们只需要求出 8/2 的最大公约数，是不是就是开头说的换了两个数再求，而我们要知道，因为两数相除，余数为0，其除数必定为最大公约数，所以这里的2也就是我们要找的134/18 的最大公约数。

快速幂（求2的幂次）

1
2
3
4
5
6
7
8
private long pow(long x, int n) {
        var res = 1L;
        for (; n > 0; n /= 2) {
            if (n % 2 > 0) res = res * x % MOD;
            x = x * x % MOD;
        }
        return res;
    }